摘要：本文将介绍排列五排除法定律，探讨其背后的原理，解析其应用方法和实际效果。该定律是一种数学原理，用于解决特定情况下的排列组合问题。本文将通过简洁明了的语言，让读者了解并理解这一定律，以便在实际问题中加以应用。

在概率论与数理统计中，排列与组合是核心部分，对于预测与决策有着广泛的应用。"排列五排除法定律"是一个重要的概念，它涉及到排列组合中的排除法思想，对于解决实际问题具有指导意义，本文将详细探讨排列五排除法定律的内涵、应用及其在实际生活中的价值。

排列五排除法定律的基本内涵

排列五排除法定律是指在处理多个元素排列的问题时，通过排除某些特定情况来简化问题的一种思想方法，当我们面临一个有多个限制条件的排列问题时，可以先不考虑这些限制条件，求出所有可能的排列情况，然后再排除不符合限制条件的情况，从而得到最终的答案，这种思想方法在数学上具有普适性，可以广泛应用于各种领域。

排列五排除法定律的应用

1、实际应用场景

排列五排除法定律在实际生活中有着广泛的应用，在彩票选号中，我们可以利用排列五排除法定律来预测可能的号码组合；在密码学中，可以通过排除法来破解密码；在生物学中，可以利用排除法来研究基因序列等。

2、具体应用步骤

在应用排列五排除法定律时，我们需要遵循以下步骤：

（1）明确问题的限制条件，确定需要排除的情况；

（2）不考虑限制条件，求出所有可能的排列情况；

（3）根据限制条件，排除不符合要求的情况；

（4）得出最终的答案。

排列五排除法定律的详细解析

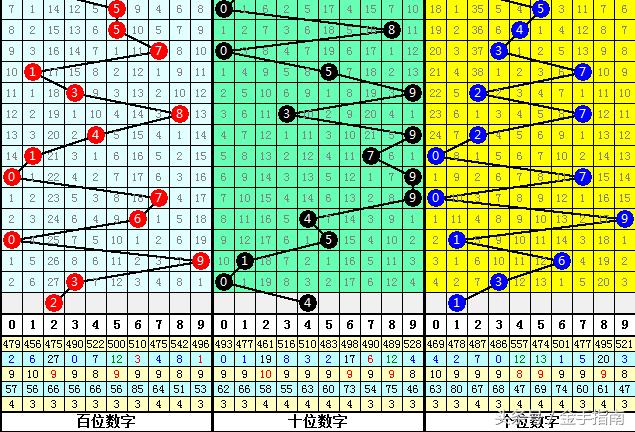
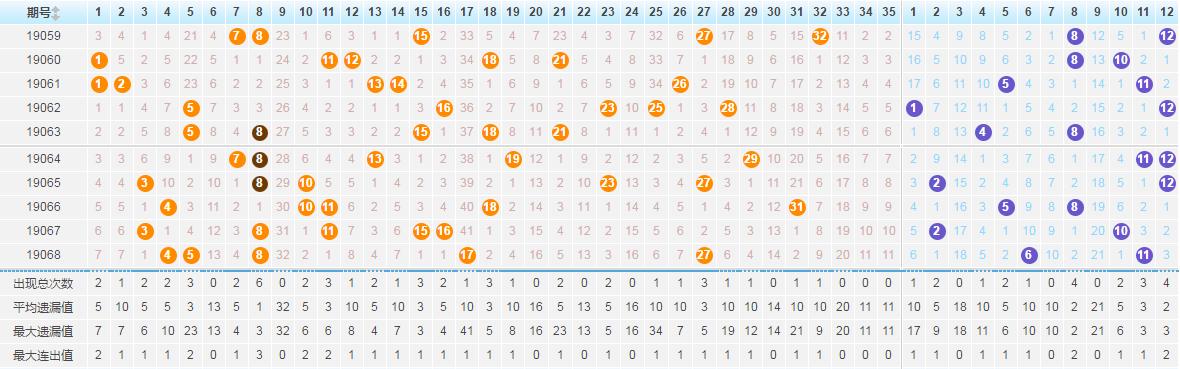
以彩票选号为例，假设我们需要从35个数字中选择5个数字进行投注，这是一个典型的排列问题，我们可以先不考虑任何限制条件，计算所有可能的组合数，然后根据历史数据、概率分析等因素，排除一些不太可能出现的数字组合，从而缩小选择范围，这就是排列五排除法定律的应用，具体步骤如下：

1、计算所有可能的组合数，不考虑限制条件，从35个数字中选择5个数字的组合数为A(35,5)。

2、根据历史数据、概率分析等因素，确定需要排除的数字组合，我们可以排除最近频繁出现的数字组合、或者长期未出现的数字组合等。

3、排除不符合要求的组合后，剩下的组合即为可能的投注号码，通过这种方式，我们可以缩小选择范围，提高中奖概率。

排列五排除法定律的优缺点及注意事项

优点：排列五排除法定律能够简化复杂问题，提高问题解决效率，通过排除不符合限制条件的情况，我们可以快速找到答案，避免陷入繁琐的计算过程，排列五排除法定律还可以帮助我们缩小选择范围，提高决策的准确性。

缺点：排列五排除法定律的应用需要一定的经验和技巧，如果不熟悉问题的背景、限制条件以及排除方法，可能会导致错误的结论，对于一些复杂问题，可能需要考虑多种限制条件，排除法可能无法完全覆盖所有情况。

注意事项：在应用排列五排除法定律时，我们需要确保所排除的情况不影响问题的本质，我们还需要注意数据的时效性和完整性，确保所依据的信息是最新、最全面的，我们还需要保持谨慎的态度，避免盲目相信排除法的结果，要结合实际情况进行综合分析。

排列五排除法定律是一种重要的思想方法，具有广泛的应用价值，通过排除不符合限制条件的情况，我们可以简化复杂问题，提高问题解决效率，应用排列五排除法定律需要一定的经验和技巧，我们需要注意其优缺点及注意事项，以确保其在实际应用中的有效性，希望通过本文的探讨，读者对排列五排除法定律有更深入的理解，并能够在实际生活中灵活运用。